Badminton Net Kill Shot

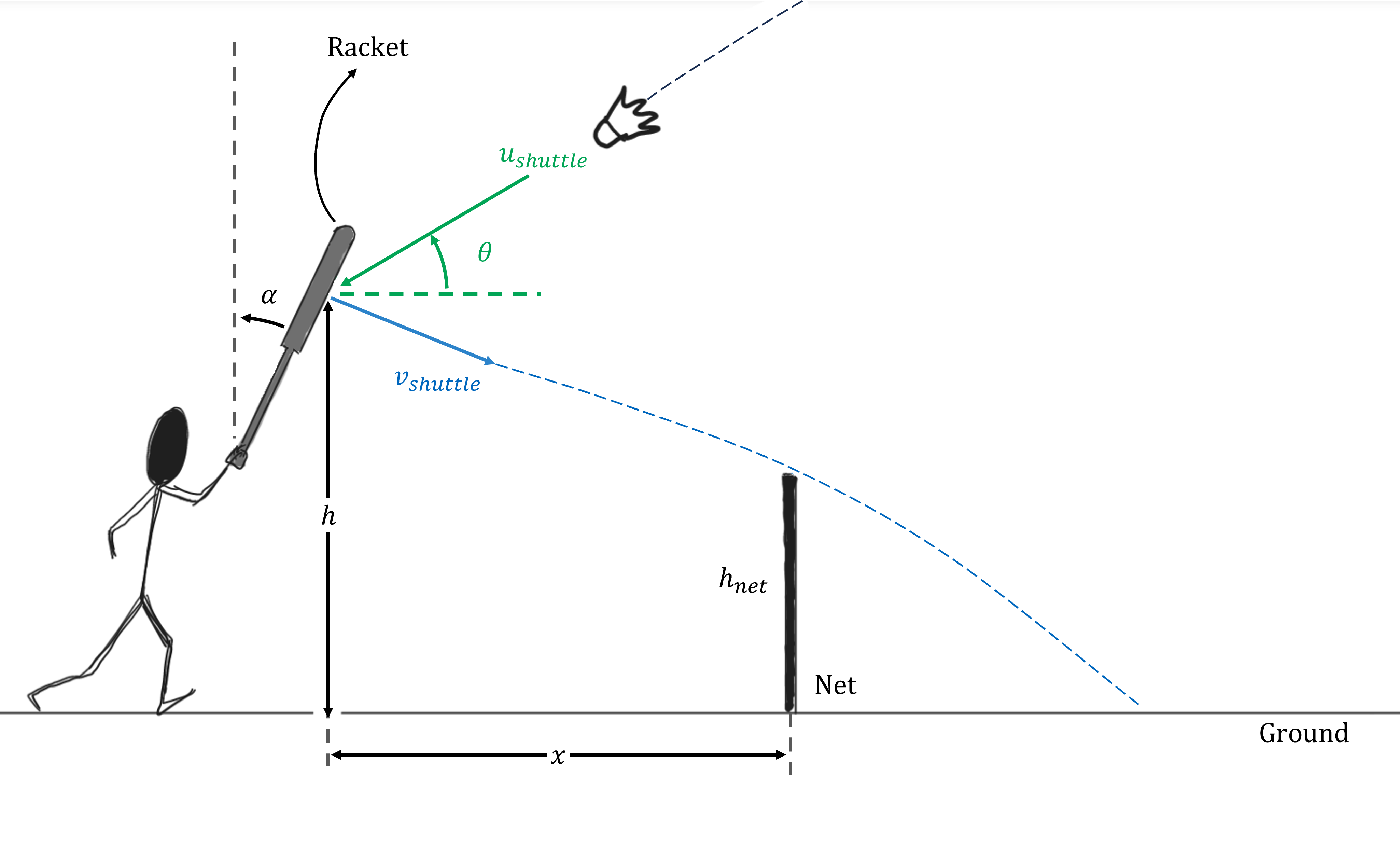
In a game of badminton, to counter a weak lift shot, the receiver can orient their racket at certain angle relative to the vertical. Thus, he/she is able to utilize the incoming momentum of the shuttle and principles of oblique impacts to return the shuttle at a steep angle without exerting an additional impulse. This agile shot is termed as a badminton net kill shot due to its play in close proximity to the net.

Part 1

Treat the racquet and shuttle as particles with masses \(1\ \rm{kg}\), \(0.1\ \rm{kg}\) respectively in a vertical plane. Assume the racquet is stationary before the collision. Neglect aerodynamic drag and effects of gravity at the point of collision.

Calculate the angle(\(\alpha\)) with which the racquet has to be oriented relative to the collision to achieve the desired trajectory as shown above.
\(\theta = {{ params.theta }}^{\circ}\), \(u\_{shuttle} = {{ params.u_s }}\ \rm{m/s}\) , \(v\_{shuttle} = {{ params.v_s }}\ \rm{m/s}\), \(h = {{ params.h }}\ \rm{m}\), \(h\_{net} = 1.524\ \rm{m}\), \(x = 1.6256\ \rm{m}\)
You may have to use the compound angle identity: \(sin(A \pm B) = sin(A)cos(B) \pm cos(A)sin(B)\)

Answer Section

Please enter in a numeric value in \(\circ\).

Part 2

Determine the the magnitude of the final velocity of the racket. Treat the badminton racket as a rigid body.

Answer Section

Please enter the value of \(v\_{racket}\) in \(\rm{m/s}\).

Part 3

Determine the coefficient of restitution(\(e\)) between the racket and the shuttle.

Answer Section

Please enter the value of \(e\).

Attribution

Problem is licensed under the CC-BY-NC-SA 4.0 license.